__Topic \#2__ __Numerical__ __ __ __analysis__ __ __ __and__ __ __ __symbolic__ __ __ __computation__  __What__ __ __ __is__ __ __ __it__ __?__ Numerical analysis Symbolic computation __Which__ __ __ __tools__ __ __ __can__ __ __ __we__ __ __ __use__ __?__  scipy  sympy  __Background __ __info__ __ – __ __David‘s__ __ __ __compendium__ __ __ __reloaded__ __\!__ [https://davrot\.github\.io/pytutorial](https://davrot.github.io/pytutorial/)[/](https://davrot.github.io/pytutorial/) __Topics:__ Sympy Numerical Integration\, Differentiation\, and Differential Equations __Which__ __ __ __mathematical__ __ __ __problems__ __ __ __are__ __ __ __we__ __ __ __interested__ __ in?__ Solving equations \(only symbolic\) Integrals over functions Derivatives of functions Solving differential equations __Numerical__ __ __ __solutions__ __ will \(__ __almost__ __\) __ __always__ __ __ __be__ __ __ __approximations__ __\! __ Precision is limited Range is limited Algorithm is approximating Errors can accumulate dramatically \(stability of algorithms\) __Examples__ __ __ __of__ __ __ __errors__ __:__ Multiplication\, one decimal place: 2\.5 \* 2\.5 = 6\.25 Addition\, 8\-bit unsigned int: 200\+200 = 400 Euler integration of ODE __\(__ __ Whiteboard\)__ __Integrals __ __over__ __ __ __functions__ __ \(‚__ __quadrature__ __‘\)__  __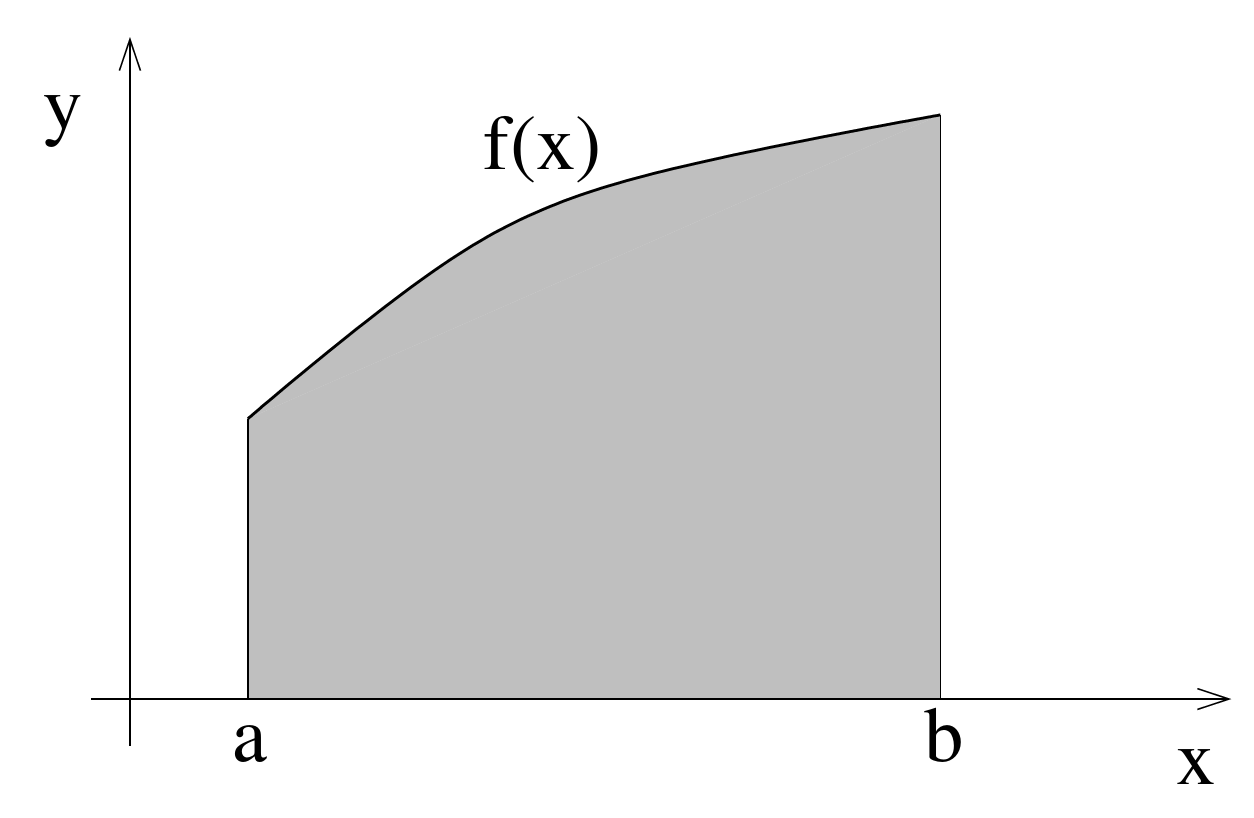Numerical__ __ __ __methods__ Integral = area under curve 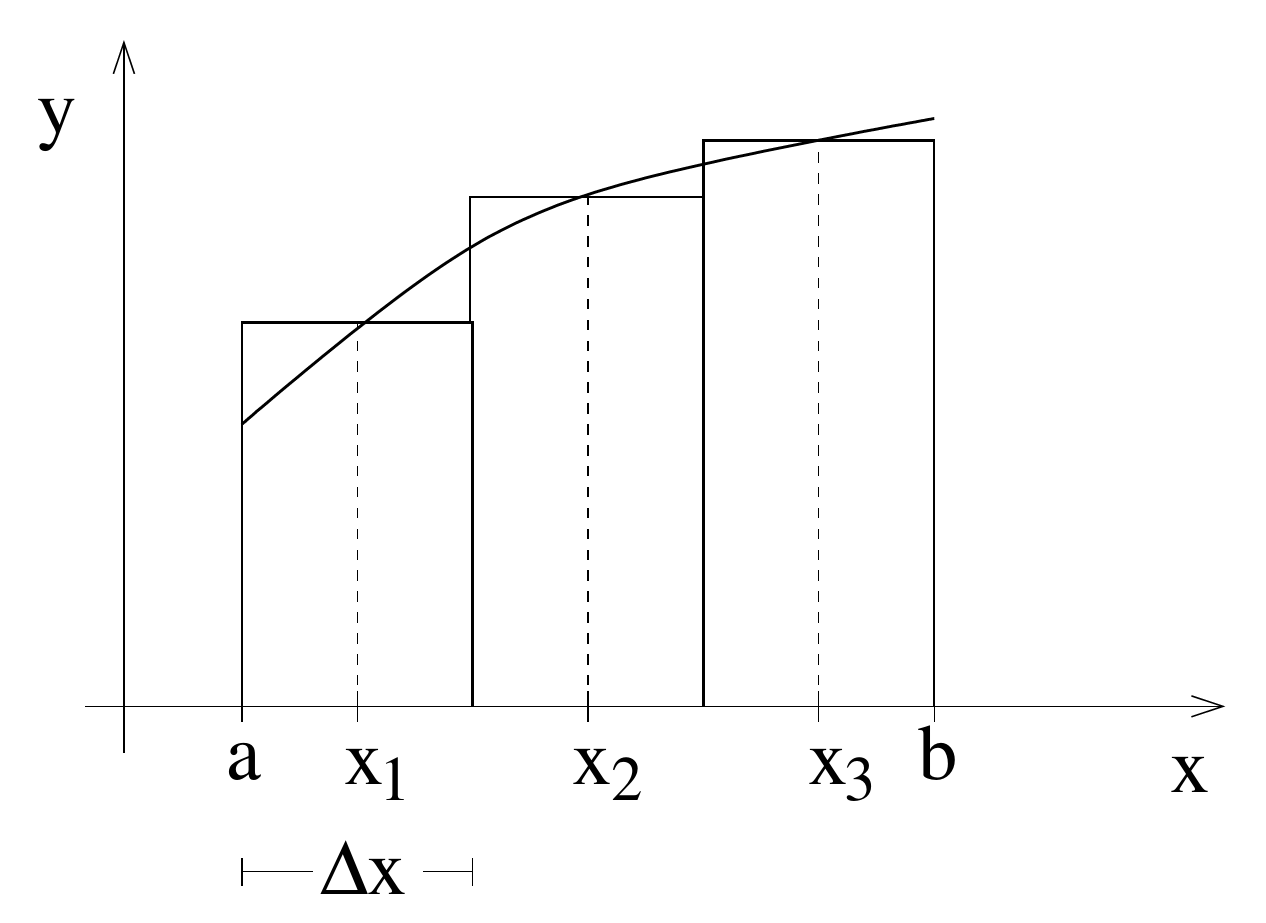Approximate area by many small boxes\, e\.g\. 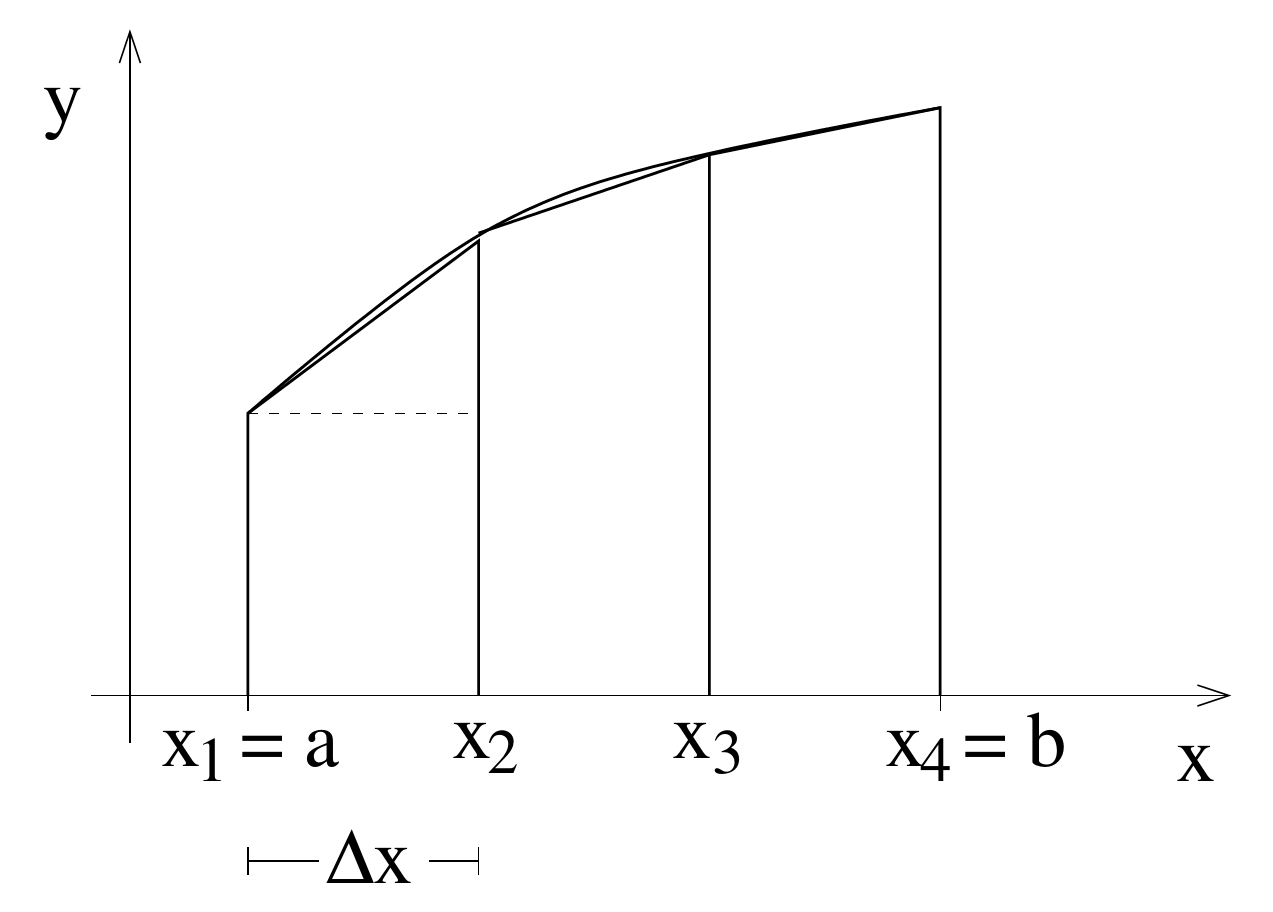by _midpoint_ _ _ _rule_ :   _Trapezoidal_ _ _ _rule_ _: _ __worse__ __ __ __than__ __ __ __midpoint__ __\!__  approximate by parabolas _Simpson‘s_ _ _ _rule_ _: _ __Numerical__ __ __ __methods__ __:__  __Symbolic__ __ __ __Methods__ We will use module __sympy__ \. For symbolic operations \(i\.e\.\, without concrete numbers\)\, we have to __declare__ __ variables/__ __symbols__ \(and later functions…\)\. For __mathematical__ __ __ __functions__ __ such __ __as__ __ cos\(…\)__ \, use the sympy equivalents \(not from math or numpy modules\!\)  For __definite __ __integrals__ \, we can specify boundaries a and b by __creating__ __ a __ __tuple__ __\(x\, a\, b\)__ for the second argument\. The solution can be __evaluated__ by using the methods __\.__ __subs__ __\(variable\, __ __value__ __\) __ to substitute a value for a variable and __\.__ __evalf__ __\(\) __ to get a numerical output\. __„Genug für heute?“__ [https://davrot\.github\.io/pytutorial/sympy/intro](https://davrot.github.io/pytutorial/sympy/intro/) [/](https://davrot.github.io/pytutorial/sympy/intro/) [https://davrot\.github\.io/pytutorial/numpy/7](https://davrot.github.io/pytutorial/numpy/7/) [/](https://davrot.github.io/pytutorial/numpy/7/) [https://davrot\.github\.io/pytutorial/numpy/8](https://davrot.github.io/pytutorial/numpy/8/) [/](https://davrot.github.io/pytutorial/numpy/8/) __Example__ __ live\-__ __coding__ __:__ integration and differentiation \, stability and instability __Differentiation __ __of__ __ __ __functions__ __Numerical__ __ __ __methods__ __:__ __centered__ __ __ __differentiation__ __right\-sided__ __ __ __differentiation__  --- Note: also important for integration of DEQs, since differential approximated by the same equations __Symbolic__ __ __ __methods__ __:__ For differentiation\, the corresponding command is __diff__ :  __Integration __ __of__ __ differential __ __equations__ __Differential __ __quotient__ __ __ __approximated__ __ __ __by__ __ finite __ __difference__ \, like in previous example\. Solution constructed by considering the following aspects: What do we want to know\, what is known? Where do we start?  __Initial __ __value__ __ __ __problem__ … How far do we step?  Smaller than fastest timescale implies __maximum__ __ __ __step__ __ __ __size__ __Warning__ __:__ differentiation / integration of functions can be performed in parallel\, differential equations require an iterative solution which can not be parallelized \! __What__ __ __ __about__ __ __ __systems__ __ __ __of__ __ differential __ __equations__ __?__ …just solve them in parallel \(see previous slide\) __Higher\-order __ __methods__ Idea: approximate differential quotient more precisely… __Solution \(Runge\-__ __Kutta__ __ 2nd __ __order__ __\):__ Go ahead with Euler by half of the stepsize… …use slope at that position for an Euler with the full stepsize\. __Numerical__ __ __ __methods__ __:__   __Symbolic__ __ __ __methods__ __:__ In addition to declaring variables\, you need… …to __declare__ __ __ __functions__ \(for the solution we are looking for\) …to __define__ __ __ __the__ __ \(differential\) __ __equation__ …and the __command__ __ __ __dsolve__ __ __ for \(trying to\) solve the DEQ:  __Symbolic__ __ __ __methods__ __\, __ __cont‘d__ __…__ For including initial conditions\, __dsolve__ __ __ has the __optional __ __argument__ __ __ __ics__ \. With __ __ __lambdify__ \, You can __convert__ __ __ __the__ __ RHS __ __of__ __ __ __the__ __ __ __solution__ __ __ __to__ __ a normal __ __numpy__ __ __ __function__ : Query the new function as to __which__ __ __ __arguments__ __ __ __it__ __ __ __takes__ \, and in which order \( __import__ __ __ __inspect__ __ __ for that purpose\)  __What__ __ __ __about__ __ partial differential __ __equations__ __?__ For example\, the cable equation:  __More __ __information__ __:__ [https://davrot\.github\.io/pytutorial/sympy/intro](https://davrot.github.io/pytutorial/sympy/intro/) [/](https://davrot.github.io/pytutorial/sympy/intro/) [https://davrot\.github\.io/pytutorial/numpy/7](https://davrot.github.io/pytutorial/numpy/7/) [/](https://davrot.github.io/pytutorial/numpy/7/) [https://davrot\.github\.io/pytutorial/numpy/8](https://davrot.github.io/pytutorial/numpy/8/) [/](https://davrot.github.io/pytutorial/numpy/8/)