mirror of
https://github.com/davrot/pytutorial.git
synced 2025-06-10 07:00:02 +02:00
|
|
||
|---|---|---|
| .. | ||
| image1.png | ||
| image2.png | ||
| image3.png | ||
| image4.png | ||
| image5.png | ||
| README.md | ||
Remove a common signal from your data
Goal
We want to remove a common signal which was mixed on top a set of data channels. There are many methods to do so. We will use SVD. Implementations are for example: scipy.linalg.svd or torch.svd_lowrank (which also works on the GPU)
Questions to David Rotermund
Creating dirty test data
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng()
time_series_length: int = 1000
number_of_channels: int = 100
t: np.ndarray = np.arange(0, time_series_length) / 1000
# Clean data
frequencies = 10 / rng.random((1, number_of_channels))
phase = 2 * np.pi * rng.random((1, number_of_channels))
clean_data: np.ndarray = (
0.5
* rng.random((1, number_of_channels))
* np.sin(t[..., np.newaxis] * 2 * np.pi * frequencies + phase)
+ np.arange(0, number_of_channels)[np.newaxis, ...]
)
# Perturbation
y: np.ndarray = np.sin(t * 2 * np.pi * 1)
mix_coefficients: np.ndarray = 1 + rng.random((number_of_channels)) * 5
perturbation: np.ndarray = y[..., np.newaxis] * mix_coefficients[np.newaxis, ...]
# Dirty data
dirty_data: np.ndarray = clean_data.copy()
dirty_data += perturbation
np.savez(
"data.npz", clean_data=clean_data, perturbation=perturbation, dirty_data=dirty_data
)
plt.plot(t, clean_data[..., 0:3])
plt.xlabel("Time [s]")
plt.ylabel("Clean data waveform")
plt.show()
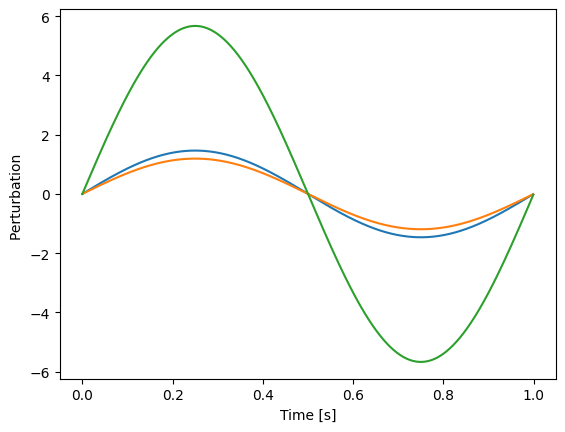
plt.plot(t, perturbation[..., 0:3])
plt.xlabel("Time [s]")
plt.ylabel("Perturbation ")
plt.show()
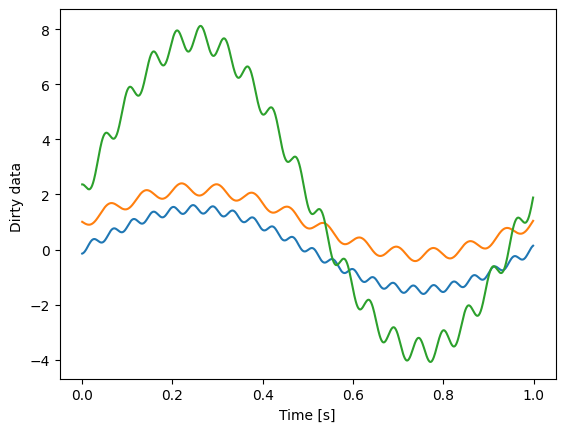
plt.plot(t, dirty_data[..., 0:3])
plt.xlabel("Time [s]")
plt.ylabel("Dirty data ")
plt.show()
Let us look at the first three of the 100 channels.
We get three fully random time series
Sine wave with random amplitudes as common perturbation
Both combined with random mixing coefficients
Estimating the common signal
import numpy as np
import scipy
import matplotlib.pyplot as plt
file = np.load("data.npz")
clean_data = file["clean_data"]
perturbation = file["perturbation"]
dirty_data = file["dirty_data"].copy()
t: np.ndarray = np.arange(0, dirty_data.shape[0]) / 1000
dirty_data -= dirty_data.mean(axis=0, keepdims=True)
u, s, Vh = scipy.linalg.svd(dirty_data, full_matrices=False)
to_remove = u[:, 0][..., np.newaxis] * Vh[0, :][np.newaxis, ...] * s[0]
dirty_data = file["dirty_data"].copy()
dirty_data -= to_remove
for i in range(0, 3):
plt.subplot(3, 1, 1 + i)
plt.plot(t, perturbation[:, i], label="original")
plt.plot(t, to_remove[:, i], "--", label="reconstructed")
plt.xlabel("Time [s]")
plt.ylabel("Perturbation ")
plt.legend(loc="upper right")
plt.show()
for i in range(0, 3):
plt.subplot(3, 1, 1 + i)
plt.plot(t, clean_data[:, i], label="original")
plt.plot(t, dirty_data[:, i], "--", label="reconstructed")
plt.xlabel("Time [s]")
plt.ylabel("clean data waveform")
plt.legend(loc="upper right")
plt.show()
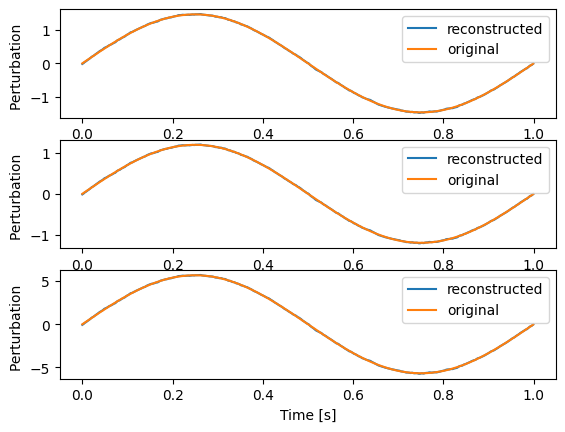
This is the original and the reconstructed pertubation for the first three channels
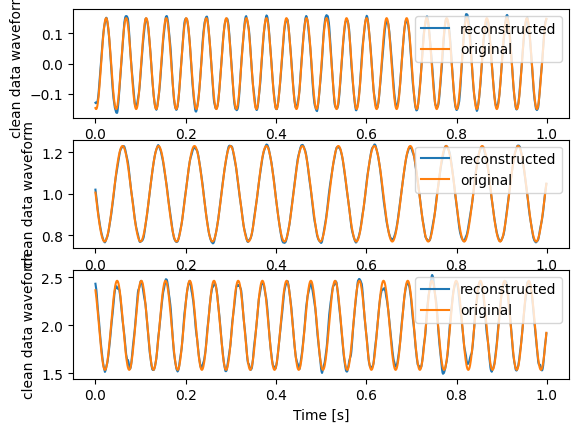
This is the original clean data and the reconstructed clean data for the first three channels