pytutorial/sympy/intro

Symbolic Computation

{:.no_toc}

* TOC {:toc}

Top

Questions to David Rotermund

pip install sympy

Overview tutorials

Basic Operations
Printing
Simplification
Calculus
Solvers
Matrices

API Reference

Basics	Contains a description of operations for the basic modules. Subcategories include: absolute basics, manipulation, assumptions, functions, simplification, calculus, solvers, and some other subcategories.
Code Generation	Contains a description of methods for the generation of compilable and executable code.
Logic	Contains method details for the logic and sets modules.
Matrices	Discusses methods for the matrices, tensor and vector modules.
Number Theory	Documents methods for the Number theory module.
Physics	Contains documentation for Physics methods.
Utilities	Contains docstrings for methods of several utility modules. Subcategories include: Interactive, Parsing, Printing, Testing, Utilities.
Topics	Contains method docstrings for several modules. Subcategories include : Plotting, Polynomials, Geometry, Category Theory, Cryptography, Differential, Holonomic, Lie Algebra, and Stats.

Basics

Assumptions
Calculus
Combinatorics
Functions
Integrals
Series
Simplify
Solvers
abc
Algebras
Concrete
Core
Discrete
Numerical Evaluation
Numeric Computation
Term Rewriting

Some examples

Substitution

import sympy

x, y = sympy.symbols("x y")

expr = sympy.cos(x) + 1
z = expr.subs(x, y**2)
print(z) # -> cos(y**2) + 1

Derivatives

import sympy

x, y = sympy.symbols("x y")

y = sympy.diff(sympy.sin(x) * sympy.exp(x), x)
print(y) # -> exp(x)*sin(x) + exp(x)*cos(x)

Integrals

import sympy

x, y = sympy.symbols("x y")

y = sympy.integrate(sympy.cos(x), x)
print(y)  # -> sin(x)

(Taylor) Series Expansion

import sympy

x, y, z = sympy.symbols("x y z")
y = sympy.cos(x)
z = y.series(x, 0, 8) # around x = 0 , up order 7

print(z)  # -> 1 - x**2/2 + x**4/24 - x**6/720 + O(x**8)

simplify

import sympy

x, y, z = sympy.symbols("x y z")
y = sympy.simplify(sympy.sin(x) ** 2 + sympy.cos(x) ** 2)

print(y)  # -> 1

Solving Equations Algebraically

solveset(equation, variable=None, domain=S.Complexes)

Recall from the gotchas section of this tutorial that symbolic equations in SymPy are not represented by = or ==, but by Eq.

import sympy

x, y, z = sympy.symbols("x y z")

z = sympy.Eq(x, y)

Output:

x=y

import sympy

x, y, z = sympy.symbols("x y z")

y = sympy.Eq(x**2 - x, 0)
z = sympy.solveset(y, x)
print(z) # -> {0, 1}

Solving Differential Equations

import sympy

# Undefined functions
f = sympy.symbols("f", cls=sympy.Function)

x = sympy.symbols("x")


diffeq = sympy.Eq(f(x).diff(x, x) - 2 * f(x).diff(x) + f(x), sympy.sin(x))

print(diffeq)  # -> Eq(f(x) - 2*Derivative(f(x), x) + Derivative(f(x), (x, 2)), sin(x))

result = sympy.dsolve(diffeq, f(x))
print(result)  # -> Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2)

Sometimes it is necessary to simplyify the problem for the solver:

import sympy

u = sympy.symbols("u", cls=sympy.Function, real=True)
t, tau, a0, urest, uc, r, i, uthr = sympy.symbols(
    "t tau a0 urest uc r i uthr", real=True
)
c0, c1, c2 = sympy.symbols("c0 c1 c2", real=True)

diffeq_rhs = (a0 * (u(t) - urest) * (u(t) - uc) + r * i) / tau

print("Original")
print(diffeq_rhs)
print()

diffeq_rhs = sympy.expand(diffeq_rhs)
diffeq_rhs = sympy.collect(diffeq_rhs, u(t))

c0_coeffs = diffeq_rhs.coeff(u(t), 0)
c1_coeffs = diffeq_rhs.coeff(u(t), 1)
c2_coeffs = diffeq_rhs.coeff(u(t), 2)

diffeq_rhs = diffeq_rhs.subs(c0_coeffs, c0)
diffeq_rhs = diffeq_rhs.subs(c1_coeffs, c1)
diffeq_rhs = diffeq_rhs.subs(c2_coeffs, c2)

print("Simplified")
print(diffeq_rhs)
print()

diffeq = sympy.Eq(u(t).diff(t), diffeq_rhs)

print("Full equation")
print(diffeq)
print()

solved_diffeq_rhs = sympy.dsolve(diffeq, u(t), ics={u(0): uc}, simplify=False).rhs

solved_diffeq_rhs = solved_diffeq_rhs.subs(c0, c0_coeffs)
solved_diffeq_rhs = solved_diffeq_rhs.subs(c1, c1_coeffs)
solved_diffeq_rhs = solved_diffeq_rhs.subs(c2, c2_coeffs)

print("Result")
print(solved_diffeq_rhs)
print()

Output:

Original
(a0*(-uc + u(t))*(-urest + u(t)) + i*r)/tau

Simplified
c0 + c1*u(t) + c2*u(t)**2

Full equation
Eq(Derivative(u(t), t), c0 + c1*u(t) + c2*u(t)**2)

Result
-t + sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*log(uc - 2*sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*(a0*uc*urest/tau + i*r/tau) + tau*sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*(-a0*uc/tau - a0*urest/tau)**2/(2*a0) + tau*(-a0*uc/tau - a0*urest/tau)/(2*a0)) - sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*log(uc + 2*sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*(a0*uc*urest/tau + i*r/tau) - tau*sqrt(-1/(4*a0*(a0*uc*urest/tau + i*r/tau)/tau - (-a0*uc/tau - a0*urest/tau)**2))*(-a0*uc/tau - a0*urest/tau)**2/(2*a0) + tau*(-a0*uc/tau - a0*urest/tau)/(2*a0))

Numerical Evaluation

import sympy

x, y = sympy.symbols("x y")

expr = sympy.cos(x) + 1
print(expr)  # -> cos(x) + 1
expr = expr.subs(x, 0.333 * sympy.pi)
print(expr)  # -> cos(0.333*pi) + 1
print(sympy.N(expr)) # -> 1.50090662536071

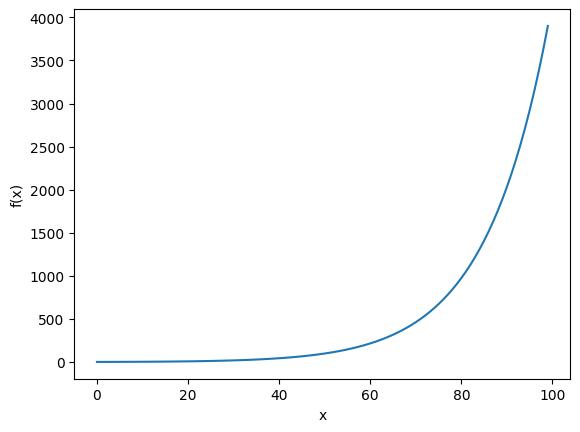
Plot your function

import sympy
import inspect
import numpy as np
import matplotlib.pyplot as plt

f = sympy.symbols("f", cls=sympy.Function)
x = sympy.symbols("x")
diffeq = sympy.Eq(f(x).diff(x, x) - 2 * f(x).diff(x) + f(x), sympy.sin(x))
result = sympy.dsolve(diffeq, f(x))

symbols = list(result.rhs.free_symbols)

f = sympy.lambdify(symbols, result.rhs, "numpy")


print("The arguments of the result:")
print(inspect.getfullargspec(f).args)
print("The source code behind f:")
print(inspect.getsource(f))

np_x = np.linspace(0, 2 * np.pi, 100)

plt.plot(f(x=np_x, C1=1.0, C2=1.0))
plt.xlabel("x")
plt.ylabel("f(x)")
plt.show()

Assumptions about the symbols

C1 = sympy.symbols('C1', positive=True)

real=True	The symbol represents a real number.
positive=True	The symbol represents a positive number.
negative=True	The symbol represents a negative number.
integer=True	The symbol represents an integer.
prime=True	The symbol represents a prime number.
odd=True	The symbol represents an odd number.
even=True	The symbol represents an even number.

Limiting the range of a symbol

import sympy

x = sympy.symbols("x")
sympy.solve([x**2 - 1, x >= 0.5, x <= 3], x)