11 KiB
11 KiB
Instantanious Spectral Coherence
{:.no_toc}
* TOC {:toc}Top
Questions to David Rotermund
Test data
import numpy as np
import matplotlib.pyplot as plt
dt: float = 1.0 / 1000.0
# I want more trials
f_base: float = 50
f_delta: float = 1
rng = np.random.default_rng(1)
n_t: int = 1000
n_trials: int = 1
t: np.ndarray = np.arange(0, n_t) * dt
amplitude: float = 0.75
x = dt * 2.0 * np.pi * (f_base + f_delta * 2 * (rng.random((n_t, n_trials)) - 0.5))
x = np.cumsum(x, axis=0)
y_a: np.ndarray = np.sin(x)
y_a[:400, :] = 0.0
y_a[-400:, :] = 0.0
y_a = y_a + amplitude * rng.random((n_t, n_trials))
y_a -= y_a.mean(axis=0, keepdims=True)
y_a /= y_a.std(axis=0, keepdims=True)
y = y_a[:, 0]
np.savez("testdata.npz", y=y, t=t)
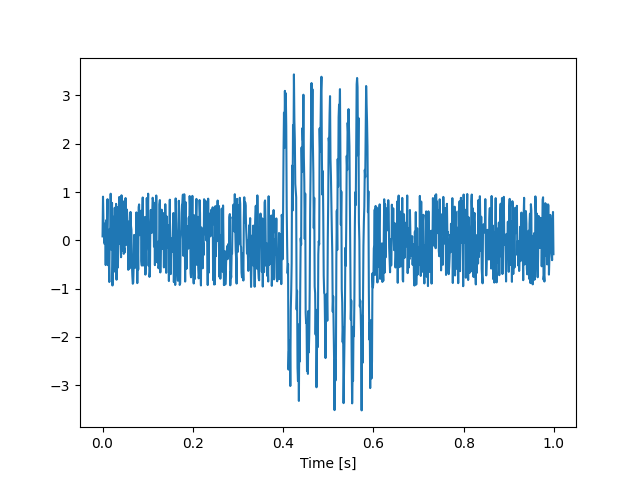
plt.plot(t, y)
plt.xlabel("Time [s]")
plt.show()
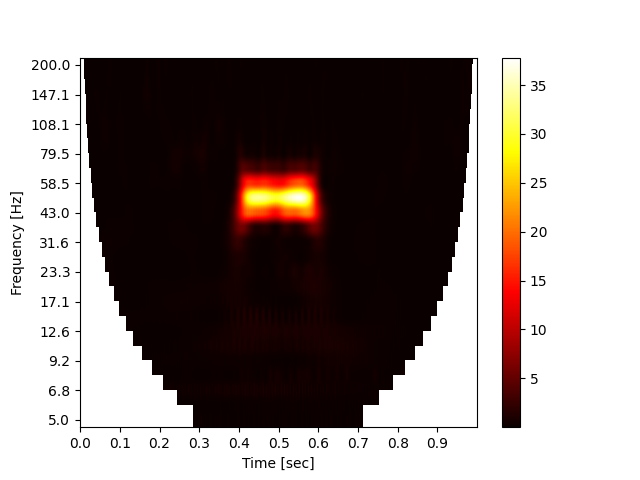
Let us look at wavelet power of the time series:
import numpy as np
import matplotlib.pyplot as plt
import pywt
# Calculate the wavelet scales we requested
def calculate_wavelet_scale(
number_of_frequences: int,
frequency_range_min: float,
frequency_range_max: float,
dt: float,
) -> np.ndarray:
s_spacing: np.ndarray = (1.0 / (number_of_frequences - 1)) * np.log2(
frequency_range_max / frequency_range_min
)
scale: np.ndarray = np.power(2, np.arange(0, number_of_frequences) * s_spacing)
frequency_axis_request: np.ndarray = frequency_range_min * np.flip(scale)
return 1.0 / (frequency_axis_request * dt)
def get_y_ticks(
reduction_to_ticks: int, frequency_axis: np.ndarray, round: int
) -> tuple[np.ndarray, np.ndarray]:
output_ticks = np.arange(
0,
frequency_axis.shape[0],
int(np.floor(frequency_axis.shape[0] / reduction_to_ticks)),
)
if round < 0:
output_freq = frequency_axis[output_ticks]
else:
output_freq = np.round(frequency_axis[output_ticks], round)
return output_ticks, output_freq
def get_x_ticks(
reduction_to_ticks: int, dt: float, number_of_timesteps: int, round: int
) -> tuple[np.ndarray, np.ndarray]:
time_axis = dt * np.arange(0, number_of_timesteps)
output_ticks = np.arange(
0, time_axis.shape[0], int(np.floor(time_axis.shape[0] / reduction_to_ticks))
)
if round < 0:
output_time_axis = time_axis[output_ticks]
else:
output_time_axis = np.round(time_axis[output_ticks], round)
return output_ticks, output_time_axis
def calculate_cone_of_influence(dt: float, frequency_axis: np.ndarray):
wave_scales = 1.0 / (frequency_axis * dt)
cone_of_influence: np.ndarray = np.ceil(np.sqrt(2) * wave_scales).astype(np.int64)
return cone_of_influence
def mask_cone_of_influence(
complex_spectrum: np.ndarray,
cone_of_influence: np.ndarray,
fill_value: float = np.NaN,
) -> np.ndarray:
assert complex_spectrum.shape[0] == cone_of_influence.shape[0]
for frequency_id in range(0, cone_of_influence.shape[0]):
# Front side
start_id: int = 0
end_id: int = int(
np.min((cone_of_influence[frequency_id], complex_spectrum.shape[1]))
)
complex_spectrum[frequency_id, start_id:end_id] = fill_value
start_id = np.max(
(
complex_spectrum.shape[1] - cone_of_influence[frequency_id] - 1,
0,
)
)
end_id = complex_spectrum.shape[1]
complex_spectrum[frequency_id, start_id:end_id] = fill_value
return complex_spectrum
t = np.load("testdata.npz")["t"]
y = np.load("testdata.npz")["y"]
dt = t[1] - t[0]
# The wavelet we want to use
mother = pywt.ContinuousWavelet("cmor1.5-1.0")
# Parameters for the wavelet transform
number_of_frequences: int = 25 # frequency bands
frequency_range_min: float = 5 # Hz
frequency_range_max: float = 200 # Hz
wave_scales = calculate_wavelet_scale(
number_of_frequences=number_of_frequences,
frequency_range_min=frequency_range_min,
frequency_range_max=frequency_range_max,
dt=dt,
)
complex_spectrum, frequency_axis = pywt.cwt(
data=y, scales=wave_scales, wavelet=mother, sampling_period=dt
)
cone_of_influence = calculate_cone_of_influence(dt, frequency_axis)
complex_spectrum = mask_cone_of_influence(
complex_spectrum=complex_spectrum,
cone_of_influence=cone_of_influence,
fill_value=np.NaN,
)
plt.imshow(abs(complex_spectrum) ** 2, cmap="hot", aspect="auto")
plt.colorbar()
y_ticks, y_labels = get_y_ticks(
reduction_to_ticks=10, frequency_axis=frequency_axis, round=1
)
x_ticks, x_labels = get_x_ticks(
reduction_to_ticks=10, dt=dt, number_of_timesteps=complex_spectrum.shape[1], round=2
)
plt.yticks(y_ticks, y_labels)
plt.xticks(x_ticks, x_labels)
plt.xlabel("Time [sec]")
plt.ylabel("Frequency [Hz]")
plt.show()
Instantanious Spectral Coherence
import numpy as np
import matplotlib.pyplot as plt
import pywt
# Calculate the wavelet scales we requested
def calculate_wavelet_scale(
number_of_frequences: int,
frequency_range_min: float,
frequency_range_max: float,
dt: float,
) -> np.ndarray:
s_spacing: np.ndarray = (1.0 / (number_of_frequences - 1)) * np.log2(
frequency_range_max / frequency_range_min
)
scale: np.ndarray = np.power(2, np.arange(0, number_of_frequences) * s_spacing)
frequency_axis_request: np.ndarray = frequency_range_min * np.flip(scale)
return 1.0 / (frequency_axis_request * dt)
def get_y_ticks(
reduction_to_ticks: int, frequency_axis: np.ndarray, round: int
) -> tuple[np.ndarray, np.ndarray]:
output_ticks = np.arange(
0,
frequency_axis.shape[0],
int(np.floor(frequency_axis.shape[0] / reduction_to_ticks)),
)
if round < 0:
output_freq = frequency_axis[output_ticks]
else:
output_freq = np.round(frequency_axis[output_ticks], round)
return output_ticks, output_freq
def get_x_ticks(
reduction_to_ticks: int, dt: float, number_of_timesteps: int, round: int
) -> tuple[np.ndarray, np.ndarray]:
time_axis = dt * np.arange(0, number_of_timesteps)
output_ticks = np.arange(
0, time_axis.shape[0], int(np.floor(time_axis.shape[0] / reduction_to_ticks))
)
if round < 0:
output_time_axis = time_axis[output_ticks]
else:
output_time_axis = np.round(time_axis[output_ticks], round)
return output_ticks, output_time_axis
def calculate_cone_of_influence(dt: float, frequency_axis: np.ndarray):
wave_scales = 1.0 / (frequency_axis * dt)
cone_of_influence: np.ndarray = np.ceil(np.sqrt(2) * wave_scales).astype(np.int64)
return cone_of_influence
def mask_cone_of_influence(
complex_spectrum: np.ndarray,
cone_of_influence: np.ndarray,
fill_value: float = np.NaN,
) -> np.ndarray:
assert complex_spectrum.shape[0] == cone_of_influence.shape[0]
for frequency_id in range(0, cone_of_influence.shape[0]):
# Front side
start_id: int = 0
end_id: int = int(
np.min((cone_of_influence[frequency_id], complex_spectrum.shape[1]))
)
complex_spectrum[frequency_id, start_id:end_id] = fill_value
start_id = np.max(
(
complex_spectrum.shape[1] - cone_of_influence[frequency_id] - 1,
0,
)
)
end_id = complex_spectrum.shape[1]
complex_spectrum[frequency_id, start_id:end_id] = fill_value
return complex_spectrum
def calculate_wavelet_tf_complex_coeffs(
data: np.ndarray,
number_of_frequences: int = 25,
frequency_range_min: float = 15,
frequency_range_max: float = 200,
dt: float = 1.0 / 1000,
) -> tuple[np.ndarray, np.ndarray, np.ndarray]:
assert data.ndim == 1
t: np.ndarray = np.arange(0, data.shape[0]) * dt
# The wavelet we want to use
mother = pywt.ContinuousWavelet("cmor1.5-1.0")
wave_scales = calculate_wavelet_scale(
number_of_frequences=number_of_frequences,
frequency_range_min=frequency_range_min,
frequency_range_max=frequency_range_max,
dt=dt,
)
complex_spectrum, frequency_axis = pywt.cwt(
data=data, scales=wave_scales, wavelet=mother, sampling_period=dt
)
return (complex_spectrum, frequency_axis, t)
def calculate_spectral_coherence(
n_trials: int,
y_a: np.ndarray,
y_b: np.ndarray,
number_of_frequences: int,
frequency_range_min: float,
frequency_range_max: float,
dt: float,
) -> tuple[np.ndarray, np.ndarray, np.ndarray]:
for trial_id in range(0, n_trials):
wave_data_a, frequency_axis, t = calculate_wavelet_tf_complex_coeffs(
data=y_a[..., trial_id],
number_of_frequences=number_of_frequences,
frequency_range_min=frequency_range_min,
frequency_range_max=frequency_range_max,
dt=dt,
)
wave_data_b, frequency_axis, t = calculate_wavelet_tf_complex_coeffs(
data=y_b[..., trial_id],
number_of_frequences=number_of_frequences,
frequency_range_min=frequency_range_min,
frequency_range_max=frequency_range_max,
dt=dt,
)
cone_of_influence = calculate_cone_of_influence(dt, frequency_axis)
wave_data_a = mask_cone_of_influence(
complex_spectrum=wave_data_a,
cone_of_influence=cone_of_influence,
fill_value=np.NaN,
)
wave_data_b = mask_cone_of_influence(
complex_spectrum=wave_data_b,
cone_of_influence=cone_of_influence,
fill_value=np.NaN,
)
if trial_id == 0:
calculation = wave_data_a * np.conj(wave_data_b)
norm_data_a = np.abs(wave_data_a) ** 2
norm_data_b = np.abs(wave_data_b) ** 2
else:
calculation += wave_data_a * np.conj(wave_data_b)
norm_data_a += np.abs(wave_data_a) ** 2
norm_data_b += np.abs(wave_data_b) ** 2
calculation /= float(n_trials)
norm_data_a /= float(n_trials)
norm_data_b /= float(n_trials)
coherence = np.abs(calculation) ** 2 / ((norm_data_a * norm_data_b) + 1e-20)
return np.nanmean(coherence, axis=-1), frequency_axis, t
# Parameters for the wavelet transform
number_of_frequences: int = 25 # frequency bands
frequency_range_min: float = 5 # Hz
frequency_range_max: float = 200 # Hz
dt: float = 1.0 / 1000.0
# I want more trials
f_base: float = 50
f_delta: float = 1
delay_enable: bool = False
# Test data ->
rng = np.random.default_rng(1)
n_t: int = 1000
n_trials: int = 100
t: np.ndarray = np.arange(0, n_t) * dt
amplitude: float = 0.75
x = dt * 2.0 * np.pi * (f_base + f_delta * 2 * (rng.random((n_t, n_trials)) - 0.5))
x = np.cumsum(x, axis=0)
y_a: np.ndarray = np.sin(x)
y_a[:400, :] = 0.0
y_a[-400:, :] = 0.0
y_a = y_a + amplitude * rng.random((n_t, n_trials))
y_a -= y_a.mean(axis=0, keepdims=True)
y_a /= y_a.std(axis=0, keepdims=True)
# <- Test data
if delay_enable:
y_b: np.ndarray = np.roll(y_a, shift=250, axis=0)
else:
y_b = y_a.copy()
coherence, frequency_axis, t = calculate_spectral_coherence(
n_trials=n_trials,
y_a=y_a,
y_b=y_b,
number_of_frequences=number_of_frequences,
frequency_range_min=frequency_range_min,
frequency_range_max=frequency_range_max,
dt=dt,
)
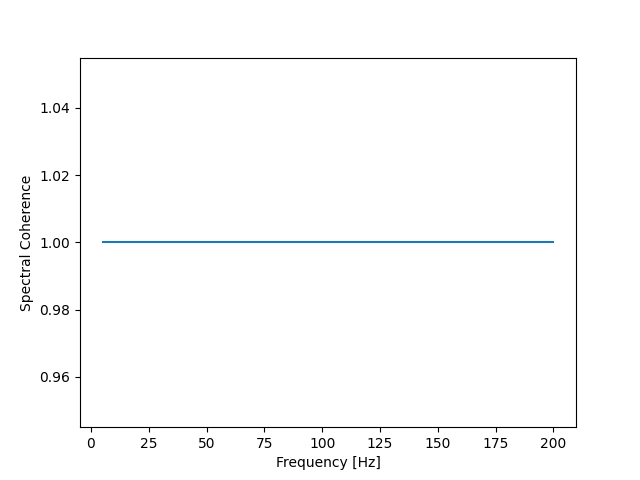
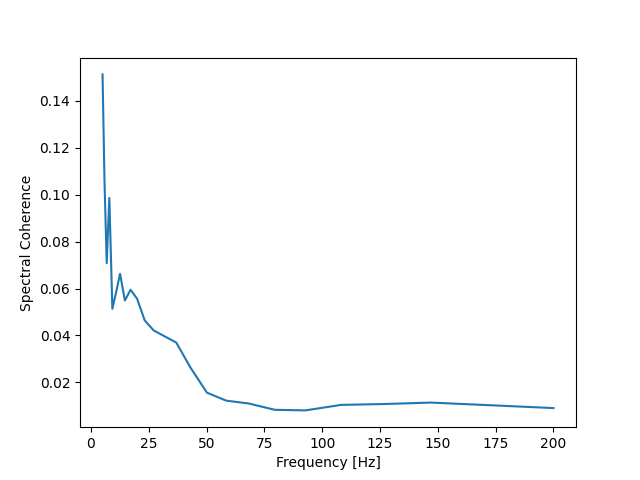
plt.plot(frequency_axis, coherence)
plt.ylabel("Spectral Coherence")
plt.xlabel("Frequency [Hz]")
plt.show()
With delay_enable = False:
With delay_enable = True: