pytutorial/scikit-learn/pca

PCA

{:.no_toc}

* TOC {:toc}

The goal

Questions to David Rotermund

Test data

import numpy as np
import matplotlib.pyplot as plt

rng = np.random.default_rng(1)

a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)

b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)

data = np.concatenate((data_a, data_b), axis=0)

angle = -0.3

roation_matrix = np.array(
    [[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]
)
data_r = data @ roation_matrix

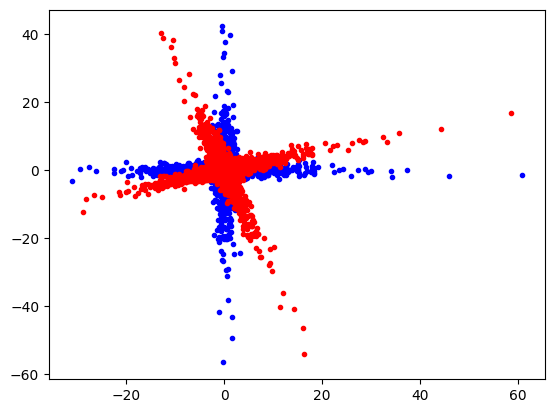
plt.plot(data[:, 0], data[:, 1], "b.")
plt.plot(data_r[:, 0], data_r[:, 1], "r.")
plt.show()

Train and use PCA​ sklearn.decomposition.PCA

class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', n_oversamples=10, power_iteration_normalizer='auto', random_state=None)

Principal component analysis (PCA).

Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.

It uses the LAPACK implementation of the full SVD or a randomized truncated SVD by the method of Halko et al. 2009, depending on the shape of the input data and the number of components to extract.

It can also use the scipy.sparse.linalg ARPACK implementation of the truncated SVD.

Notice that this class does not support sparse input. See TruncatedSVD for an alternative with sparse data.

Attributes

explained_variance_ : ndarray of shape (n_components,) The amount of variance explained by each of the selected components. The variance estimation uses n_samples - 1 degrees of freedom.

Equal to n_components largest eigenvalues of the covariance matrix of X.

singular_values_ : ndarray of shape (n_components,) The singular values corresponding to each of the selected components. The singular values are equal to the 2-norms of the n_components variables in the lower-dimensional space.

Methods:

fit(X, y=None)

X : array-like of shape (n_samples, n_features)

Training data, where n_samples is the number of samples and n_features is the number of features.

transform(X)

Apply dimensionality reduction to X.

X is projected on the first principal components previously extracted from a training set.

X : array-like of shape (n_samples, n_features)

New data, where n_samples is the number of samples and n_features is the number of features.

We rotate the red cloud back. This creates the black cloud. ​This fits nicely with the original data (blue cloud).

Be aware that the sign of an ​individual axis can switch!!!​

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

rng = np.random.default_rng(1)

a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)

b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)

data = np.concatenate((data_a, data_b), axis=0)

angle = -0.3

roation_matrix = np.array(
    [[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]
)
data_r = data @ roation_matrix


pca = PCA(n_components=2)

# Train
pca.fit(data_r)

print(pca.explained_variance_ratio_)  # -> [0.52996112 0.47003888]
print(pca.singular_values_)  # -> [287.55360494 270.80938189]

# Use
transformed_data = pca.transform(data_r)


plt.plot(data[:, 0], data[:, 1], "b.")
plt.plot(data_r[:, 0], data_r[:, 1], "r.")
plt.plot(transformed_data[:, 0], transformed_data[:, 1], "k.")
plt.show()