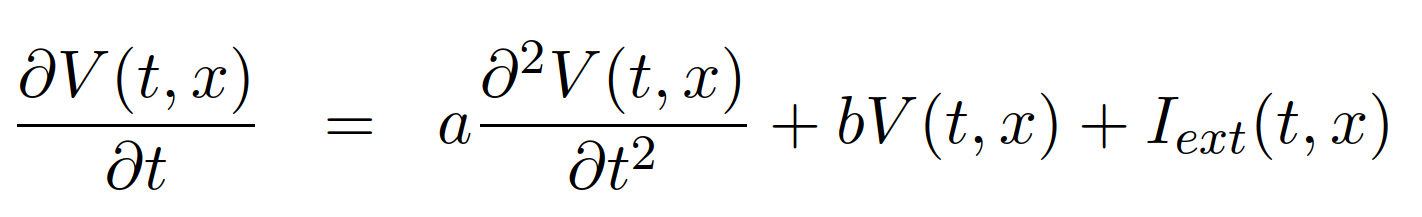11 KiB
Topic #2 Numerical __ __ analysis __ __ and __ __ symbolic __ __ computation
What __ __ is __ __ it ?
Numerical analysis
Symbolic computation
Which __ __ tools __ __ can __ __ we __ __ use ?
scipy
sympy
__Background __ info __ – __ David‘s __ __ compendium __ __ reloaded !
https://davrot.github.io/pytutorial/
Topics:
Sympy
Numerical Integration, Differentiation, and Differential Equations
Which __ __ mathematical __ __ problems __ __ are __ __ we __ __ interested __ in?__
Solving equations only symbolic
Integrals over functions
Derivatives of functions
Solving differential equations
Numerical __ __ solutions __ will __ __almost__ __ __ always __ __ be __ __ approximations __! __
Precision is limited
Range is limited
Algorithm is approximating
Errors can accumulate dramatically stability of algorithms
Examples __ __ of __ __ errors :
Multiplication, one decimal place: 2.5 * 2.5 = 6.25
Addition, 8-bit unsigned int: 200+200 = 400
Euler integration of ODE ( Whiteboard)
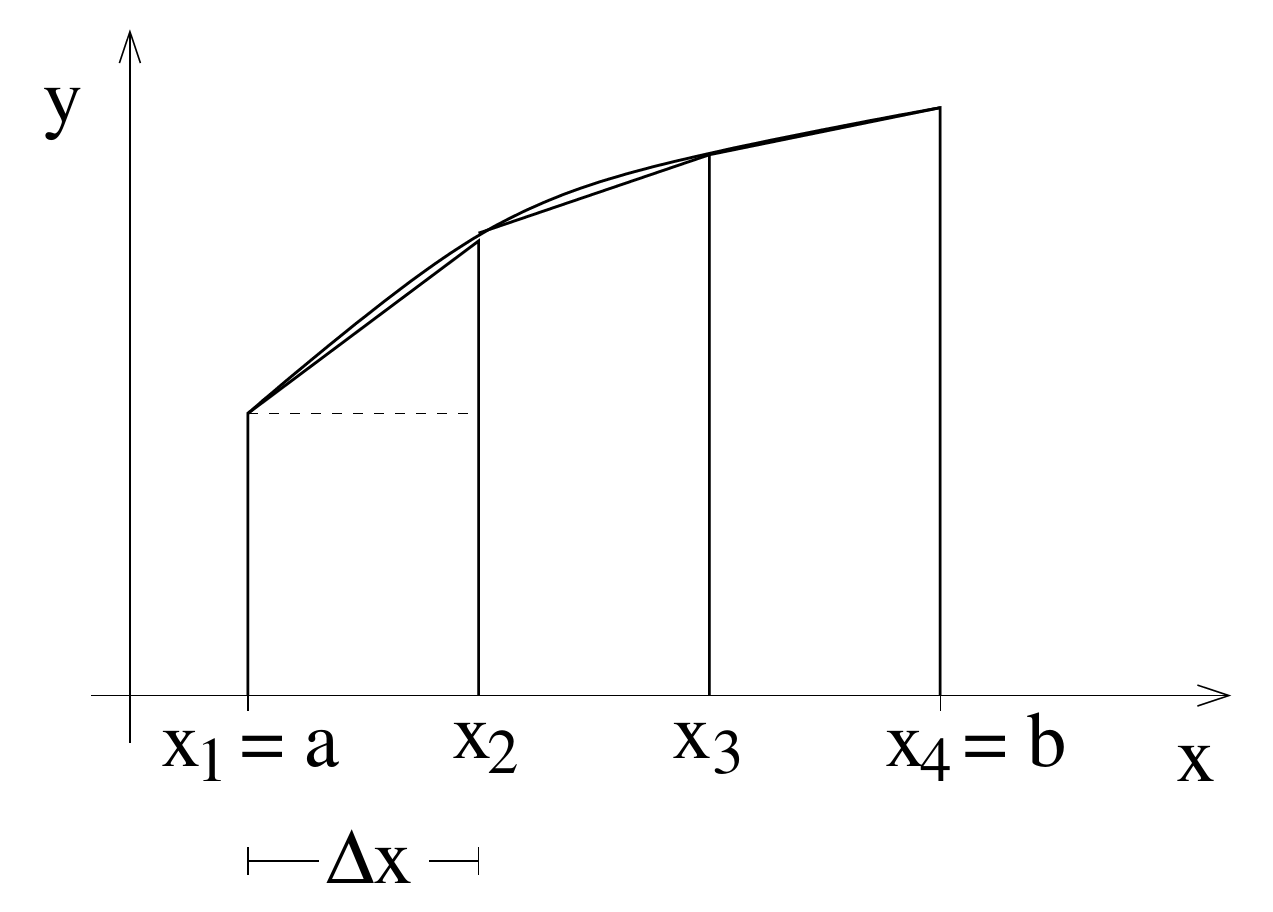
Integrals __ over __ __ functions __ (‚ quadrature ‘)
Numerical __ __ methods
Integral = area under curve
Approximate area by many small boxes, e.g. by midpoint _ _ rule :
Trapezoidal _ _ rule _: _
worse __ __ than __ __ midpoint !
approximate by parabolas
Simpson‘s _ _ rule _: _
Numerical __ __ methods :
Symbolic __ __ Methods
We will use module sympy .
For symbolic operations (i.e., without concrete numbers), we have to declare __ variables/__ symbols (and later functions…).
For mathematical __ __ functions __ such __ as __ cos(…)__ , use the sympy equivalents not from math or numpy modules\!
For __definite __ integrals , we can specify boundaries a and b by creating __ a __ tuple (x, a, b) for the second argument.
The solution can be evaluated by using the methods . subs __variable\, __ </span> <span style="color:#0070C0"> __value__ </span> <span style="color:#0070C0"> __ __ to substitute a value for a variable and . evalf __ __ to get a numerical output.
„Genug für heute?“
https://davrot.github.io/pytutorial/sympy/intro /
https://davrot.github.io/pytutorial/numpy/7 /
https://davrot.github.io/pytutorial/numpy/8 /
Example __ live-__ coding : integration and differentiation , stability and instability
__Differentiation __ of __ __ functions
Numerical __ __ methods :
centered __ __ differentiation
right-sided __ __ differentiation
Note: also important for integration of DEQs, since differential approximated by the same equations
Symbolic __ __ methods :
For differentiation, the corresponding command is diff :
__Integration __ of __ differential __ equations
__Differential __ quotient __ __ approximated __ __ by __ finite __ difference , like in previous example. Solution constructed by considering the following aspects:
What do we want to know, what is known?
Where do we start? __Initial __ value __ __ problem …
How far do we step? Smaller than fastest timescale implies maximum __ __ step __ __ size
Warning :
differentiation / integration of functions can be performed in parallel,
differential equations require an iterative solution which can not be parallelized !
What __ __ about __ __ systems __ __ of __ differential __ equations ?
…just solve them in parallel see previous slide
__Higher-order __ methods
Idea: approximate differential quotient more precisely…
Solution Runge\-__ __Kutta__ __ 2nd __ __order__ __:
Go ahead with Euler by half of the stepsize…
…use slope at that position for an Euler with the full stepsize.
Numerical __ __ methods :
Symbolic __ __ methods :
In addition to declaring variables, you need…
…to declare __ __ functions for the solution we are looking for
…to define __ __ the __ differential __ equation
…and the command __ __ dsolve __ __ for trying to solve the DEQ:
Symbolic __ __ methods __, __ cont‘d …
For including initial conditions, dsolve __ __ has the __optional __ argument __ __ ics .
With __ __ lambdify , You can convert __ __ the __ RHS __ of __ __ the __ __ solution __ __ to __ a normal __ numpy __ __ function :
Query the new function as to which __ __ arguments __ __ it __ __ takes , and in which order <span style="color:#0070C0"> __import__ </span> <span style="color:#0070C0"> __ __ </span> <span style="color:#0070C0"> __inspect__ </span> <span style="color:#0070C0"> __ __ </span> for that purpose
What __ __ about __ partial differential __ equations ?
For example, the cable equation:
__More __ information :
https://davrot.github.io/pytutorial/sympy/intro /